Vibration plays an all-embracing role in the overall field of dynamic mechanical loading on torque sensors, since even though it does not as a rule cause dynamic load components in its own right, it does act as an amplifying mechanism. Certainly it is often the deciding factor when trying to answer the question about whether a certain dynamic load will actually lead to a critical operating status, and if so in what frequency band. This applies both to a loading due to a dynamic torque and to dynamically operating parasitic loads such as rotating bending moments.
Vibrational properties are always system properties, for which reason the frequently asked question about the natural mechanical frequencies of torque sensors does not go far enough. On the contrary, a configuration such as a test bench must be investigated as a whole. This chapter therefore concentrates chiefly on the available options for computing and estimating natural frequencies.
A critical operating status is always to be expected when a natural frequency coincides with the frequency of an excitation, in other words when resonance is present. It should be noted in such a case that many periodic excitations are not precisely in the form of a sinusoidal motion. As can be verified with the aid of the Fourier series expansion, the fundamental frequency of the excitation can be accompanied by multiples of this frequency in the excitation spectrum.
Whether a resonance actually leads to a critical operating status depends on the amplitude with which the frequency concerned occurs in the excitation spectrum. The second deciding factor is the damping of this natural frequency, which is a system property. Damping is in any case very difficult to take into consideration in advance at the layout and design stage, since a decisive component often stems from complex effects such as in the fitting points.
1 Torsional Vibration
Simple mathematical mechanical models
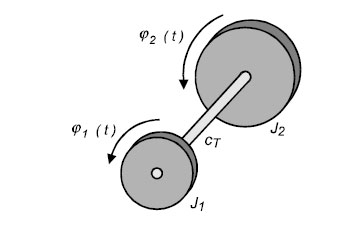
In the case of torsional vibration, the vibrational motion is a torsion about the axis of rotation. A particularly simple system that can exhibit torsional vibration is shown in Fig. 4.8, where a massless torsion rod with torsional stiffness cT is firmly fixed at one end, and supports a disk with mass moment of inertia J at the other end. As mentioned above, damping is initially disregarded during modeling, since quantitative determination on the basis of physical effects such as bearing friction, air friction and processes within joints and couplings is very difficult.
In the case of torsional vibration, the vibrational motion is a torsion about the axis of rotation. A particularly simple system, where a massless torsion rod with torsional stiffness cT is firmly fixed at one end, and supports a disk with mass moment of inertia J at the other end. As mentioned above, damping is initially disregarded during modeling, since quantitative determination on the basis of physical effects such as bearing friction, air friction and processes within joints and couplings is very difficult.
Thus if the occurrence of resonance can be attributed to particular speeds, we refer to these as critical speeds, and here especially we say that such speeds are torsionally critical.
The effect that torsional vibration has on the torque actually operating in the shaft train, and what effect if any it has on the measured torque, depends on various factors.
2 Bending Vibration
Bending vibration in rotating machines frequently leads to considerable difficulties. However, it has secondary importance when torque is being measured, because its effect on the measurement signal is small. Although this is still commonly believed, there is practically no relevant link between bending and torsional vibration (except in special cases such as crankshaft drives, where the link is obvious). However, bending vibration has a strong influence on parasitic loads, especially bending moments and radial forces. Bending vibration is thus frequently the cause of initially inexplicable components in the torque measurement signal which can be traced back to the cross-talk explained above, and is often also the cause of overloading, and occasionally even the mechanical destruction of the torque sensor. Some of the possible excitation mechanisms for bending vibration are:
- Unbalance
- Shaking motions
- Acceleration of the oscillating masses in crankshaft drives and connecting rods
- Periodic aerodynamic forces
- Dynamic instability (self-excited vibration)
- Periodic sag as a consequence of rotationally asymmetrical bending stiffness
As with oscillating torque, excitation frequencies are often proportional to the speed. Not uncommonly a particular or frequently occurring ratio of excitation frequency to speed can be the result of a special excitation mechanism.
3 Axial Vibration
Axial vibration in rotating machinery is rather rare because the chief mechanisms in such machines have few links to axial forces and motion. Thus there are few excitation mechanisms. A possible excitation, however, can stem from lever mechanisms that convert an axial force component into a torque. There have also been reports of vibrations arising from parameter excitation. This is due to the fact that the axial stiffness of elastic couplings is dependent on bending pre-tensioning. If this bending pre-tensioning is due to an alignment error, its spatial orientation relative to the rotating system is changing over time. This oscillating, time-related stiffness parameter can give rise to vibrations. If axial vibrations occur, they can very easily lead to problems because on the one hand they are often not acquired by the measurement technology and remain unnoticed until damage occurs, and on the other because many bearing designs can accept only a low axial end thrust. Also many couplings, such as concentric ring couplings, are critical relative to axial vibration since they exhibit low axial stiffness. High-amplitude axial vibrations can therefore lead to jolting and may result in irregular loading.